2019年1月頃、ル・クリントのランプシェードにインスパイアされて、こんな照明カバーを作りました。
(写真は、2020年4月に微調整して場所移動したときに撮影)

で、このとき使ったプラスチック障子紙、何故か2枚入りを買ったので、1枚で足りて、1枚余っていました。

これを有効利用したいものです。
もうひとつ、作ろう。
今度は、お店で見たこれを作ってみたい・・・。

紙を折って、球体ができるなんて、不思議です。
前は、適当に自己流で作りましたが、今度はなるべく同じものを作りたいです。
どういう設計になっているのだろうか。
じーっと観察してみると・・・


左側が前に自作したもの。右が今回作りたい球体。
ヒダヒダの形状というか、構成する多角形の形が異なります。
左は縦の線が、山になったり谷になったりしているし、縦に細長い6角形で構成されています。
右は縦の線がすべて谷折り。そして菱形で構成されています。
図にするとこんな感じ。

左が前につくったもの、右がこれから作りたい球体。
右は、菱形で構成されています。
実際に紙を折ってみながら確認すると・・・
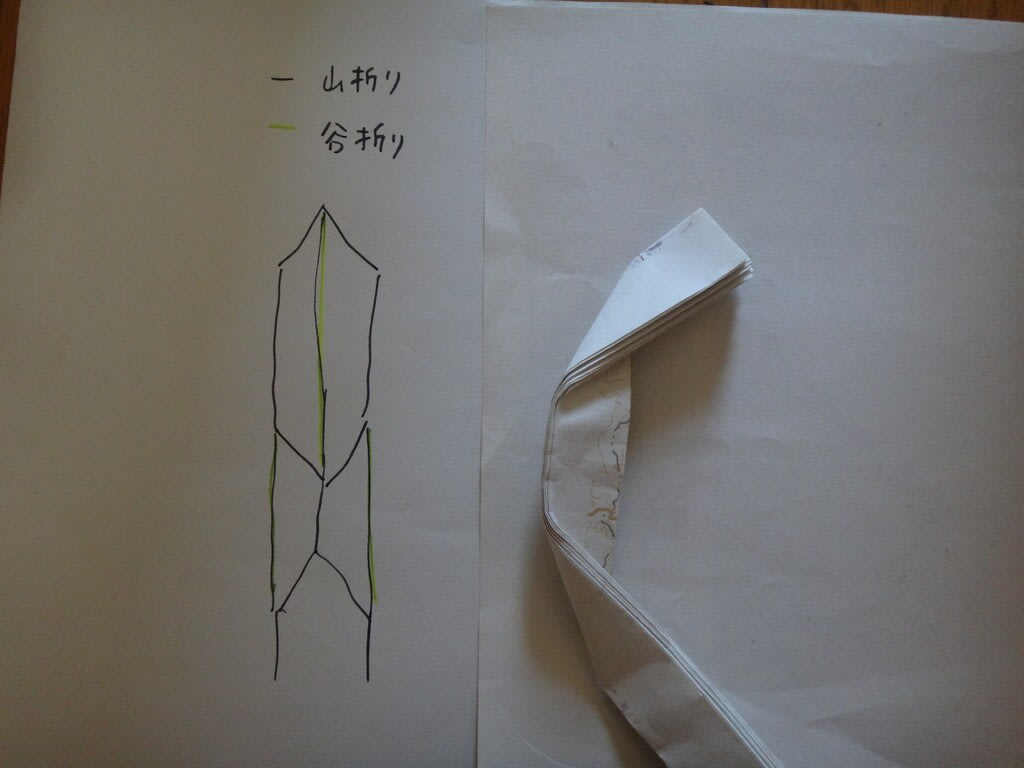
こういう折り方でつくると、表面が六角形になってきます。

こういう折り方だと、菱形で構成されることになります。
こうやって屏風畳みの紙を、斜め線が連続するようにに何度か折って、半円をつくるようにする、ということ。
適当に折ってみて思ったのですが、作りたいサイズと、屏風畳みの幅は関係しているような気がします。
適当な幅の屏風畳みを適当に折ったのでは、丸くなっていかないような・・・。
(前に作った時は、適当な幅の屏風畳みを適当に折っただけだった・・・・)
で、うまいこと説明できませんが、正多角形を作るためには、次のような法則があることが分かりました。
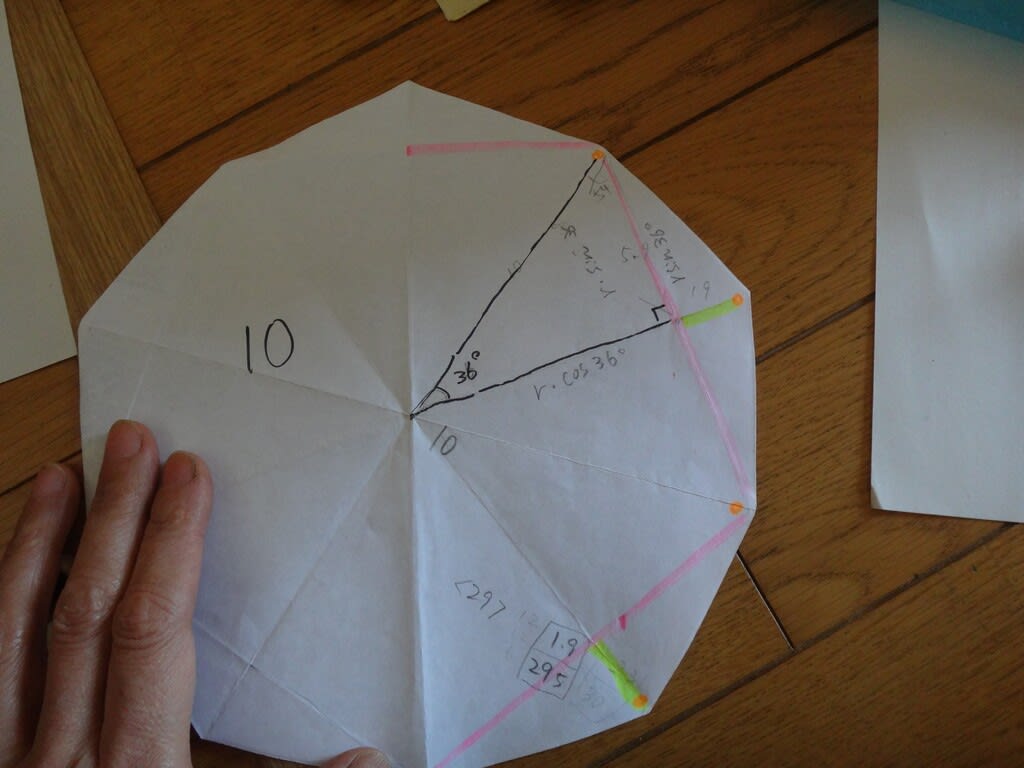
例えば、投影したときに正10角形になるようなボールを作るには、
・屏風畳みの幅は、蛍光イエローの部分
・紙の長さに相当するのは、頂点を一個飛ばしにした部分の長さ、つまり蛍光ピンクの部分の長さ
となります。
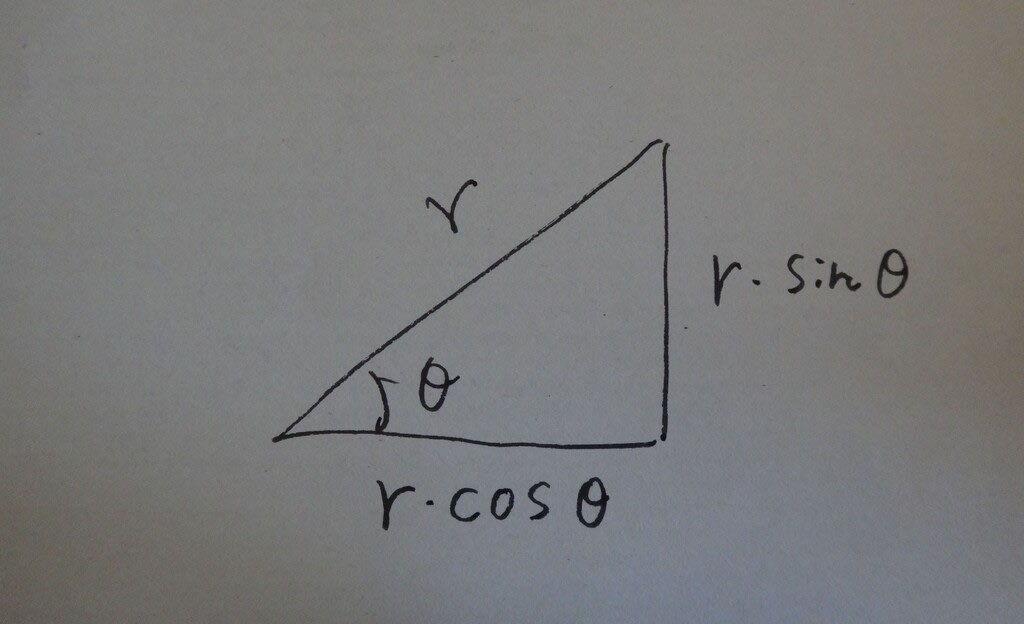
直角三角形の各辺の長さは、こういう計算です(グーグル先生、ありがとう!)。
半径rの正2n角形にしたい場合、
中心角θ=360/2n
紙の縦の長さ=r・sinθ x n
屏風畳みの幅=r-r・cosθ
紙の横幅=ヒダの角度60度とすると円周の約2倍=2×2πr
実際にやってみます。
(うっとおしかったら数式の部分は飛ばしちゃって、写真だけ見て下さいませ)
■正6角形の場合
半径10cmの正6角形とすると
θ=360/6 =60
紙の縦の長さ=10・sin60° x 3
=10・0.87 x 3
≒26.0
屏風畳みの幅=r-r・cosθ
=10-10・0.5
=5



26cmの長さ(×横幅約125cmもしくはもっと)の紙を、5cm幅に折り畳み、26cmが3区分になるように斜め線を入れて菱形を作って畳むと、投影形状が6角形のボールになります。
(ヒダが粗くてボールとは呼べないかもしれませんが)
(写真はテストピースなので横幅30cm程度でつくっています)
■正8角形の場合
半径10cmの正8角形の場合
θ=360/8 =45°
紙の縦の長さ=10・sin45° x 4
=10・0.71 x 4
≒28.4
屏風畳みの幅=r-r・cosθ
=10-10・0.707
=2.9



28.4cmの長さ(×横幅約127.6cmもしくはもっと)の紙を、2.9cm幅に折り畳み、28.4cmが4区分になるように斜め線を入れて菱形を作って畳むと、投影形状が8角形のボールになります。
(写真はテストピースなので横幅30cm程度でつくっています)
■正10角形の場合
半径10cmの正10角形の場合
θ=360/10 =36
紙の縦の長さ=10・sin36° x 5
=10・0.59 x 5
≒29.5
屏風畳みの幅=r-r・cosθ
=10-10・0.81
=1.9



29.5cmの長さ(×横幅約125.4cmもしくはもっと)の紙を、1.9cm幅に折り畳み、29.5cmが5区分になるように斜め線を入れて菱形を作って畳むと、投影形状が10角形のボールになります。
(写真はテストピースなので横幅30cm程度でつくっています)
だいぶボールぽくなってきました。
■正12角形の場合
半径10cmの正12角形の場合
θ=360/12 =30°
紙の縦の長さ=10・sin30° x 6
=10・0.5 x 6
=30
屏風畳みの幅=r-r・cosθ
=10-10・0.866
=1.34



30cmの長さ(×横幅約126cmもしくはもっと)の紙を、1.34cm幅に折り畳み、30cmが6区分になるように斜め線を入れて菱形を作って畳むと、投影形状が12角形のボールになります。
とてもヒダが浅くなってきました。
作りたい球体は、写真をじーっとにらんで数えてみると、最後の12角形だと思います。
半径25cm、直径50cmくらいでちょうど、照明器具を中にいれられるし、障子紙の縦の長さ90cmにおさまりそうです。

実物大投影モデル。
半径25cmの正12角形の場合
θ=360/12 =30°
紙の縦の長さ=25・sin30° x 6
=25・0.5 x 6
=75
屏風畳みの幅=r-r・cosθ
=25-25・0.866
=3.35
紙の横幅=2×2πr
=2×2・3.14・25
=314
紙の縦の長さは、90cmにおさまるし、ヒダの幅は、3.3cmでよさそう。
横幅は、計算上は180cmの2枚分、360cmはなくてもよさそうですが、丁度2枚分加工することにします。
1枚買い足すことになります。
これにあうような感じで、まずは実物大サンプルを作っていきます。
(続く)